cfla's blog

数字逻辑课程

发表于 更新于 分类于 阅读次数： Valine：

数字逻辑

第一章 逻辑代数基础

1.1 布尔代数

也叫逻辑代数，开关代数，以后不作区分。是一种定义在{0，1}上的代数系统，表示为(K, +, ·, -, 0, 1)。

· + - 分别对应 ∧∨ ┐，与或非，合取、析取、非。

虽然课本上这样写，但我觉得根据离散数学里学的代数系统的知识，代数系统是 非空集合 加上定义在集合上的运算，所以应该写成 ({0, 1}, +, ·, -) 。

· 即合取，可以像乘号一样省略。

逻辑代数公理：

  1. 0 - 1 律

    1
    2
    3
    4
    A + 0 = A
    A + 1 = 1
    A · 0 = 0
    A · 1 = A

  2. 重叠律

    1
    2
    A + A = A
    A · A = A

  3. 互补律

    1
    2
    A + ┐A = 1
    A · ┐A = 0

  4. 对合律

    1
    ┐┐A = A

  5. 交换律

  6. 结合律

  7. 分配律

    1
    2
    A · (B + C) = AB + AC  与对或的分配
    A + BC = (A + B)(A + C) 或对与的分配

1.2 逻辑函数

定义: 从n个逻辑变量到01的映射。记为F = f(A1, A2, A3 … )

逻辑函数有三种表示法和两种标准形式（最小项表达式和最大项表达式）

1.2.1 三种表示法：

  1. 逻辑表达式：类似数学表达式，由逻辑变量和运算符按一定规律组合而成

  2. 真值表

  3. 卡诺图

    用图形表示逻辑函数的方法，在使函数值为1的变量组合所对应的小方格上标记1。

    挖坑 卡诺图应该和最小项表达式有关，等学了再填坑。

1.2.2 两种标准形式

最小项表达式：也叫积之和范式 或 主析取范式

最小项的定义：由若干项乘积之和组成，其中每个乘积项包含该函数的全部逻辑变量，或以原变量的形式出现，或以反变量的形式出现，且每个变量在一个乘积项中只出现一次。

最小项的表示：

对于n个变量而言，可以构成2的n次方个最小项。这个性质类似与n位二进制数有2的n次方种组合，因此我们可以对最小项表达式作出规定，以便方便的表示他们。

对于一个n变量的最小项表达式，当各个变量按一定次序排好后，用1代表原变量，用0代表反变量，这样一个最小项表达式可以被转化为2进制数，我们用 m~i~ 来表示这个最小项表达式。

Q：为什么要使用1代表原变量，用0代表反变量？

A：如果有一个最小项mi，如果令原变量为1，反变量为0，一定能使mi = 1，而且这是唯一的。

例如m6 = AB┐C，其顺序为110B = 6D，令对应的逻辑变量为1或0，则m6 = 1 · 1 · (┐0) = 1

例如，最小项表达式 AB, 转换成二进制即11，表示为m3。

最小项表达式A┐B，转换成二进制即10，表示为m2。

最小项的性质：

  • 对于任意一个最小项，只有一组变量取值可以使其值为1
  • 任意两个最小项之积为0
  • n个变量的所有2^n^ 个最小项之和为1

将任意表达式转换为最小项表达式：

利用公式A = A(B + ┐B)

最小项表达式的性质：

  • 性质1：若m~i~是逻辑函数 F(A1 ,A2 ,…,An ) 的一个最小项，则使mi=1的一组变量取值 (a1 ,a2 ,…,an ) 必定使 F 值为 l 。
  • 性质2：若 F1 和 F2 都是 A1 ,A2 ,…,An 的函数，则 F=F1+F2 将包括 F1 和 F2 中的所有最小项， G=F1·F2 将包括 F1 和 F2 中的公有最小项。
  • 性质3：若 F 是 ┐F 的反函数，则F必定由F所包含 的最小项之外的全部最小项所组成

思考题：任何n变量的逻辑函数都有且仅有一个最小项表达式

使用归谬法证明

第一次课到此结束

最大项表达式： 也叫和之积范式或主合取范式

定义：设n个逻辑变量，他们所组成的和项（“或”项）中，每个变量或以原变量或以反变量形式出现，且仅出现一次，这个和项称为n变量的最大项。

举例：

二变量最大项表达式：（A + B），（A + ┐B）, (┐A + B), (┐A + ┐B)

三变量最大项表达式：

最大项表达式的三条性质类似最小项表达式的三条性质：

  1. 对于任意一个最大项，只有一组变量取值可使其值为0。
  2. 任意两个最大项 Mi 和 Mj 之和必为1。
  3. n 变量的所有2^n^ 个最大项之积必为0。

最大项表达式以 + 连接，因此绝大多数的最大想表达式的值为1，但是对于任意一个最大项，只有一组变量取值可使其值为0。

任意逻辑表达式转换成最大项表达式：

先用“或对与的分配”（就是普通加减乘除代数没有的那种分配律），将给定逻辑表达式展开为 “或 - 与” 表达式，然后对每一个或项“或”上 （加上） 所缺变量x的 x┐x。

类似(A + B)(A + ┐B) ，先在括号里进行或运算，再在括号外进行与运算的表达式，被称为“或 - 与” 表达式。

AB + A┐B, 而这种表达式被称为 “与 - 或”表达式

最大项表达式的性质也与最小项表达式类似：

  • 性质1：若Mi是逻辑函数F(A1 ,A2 ,…,An )的一个 最大项，则使Mi=0的一组变量取值(a1 ,a2 ,…,an ) 必定使F值为0。
  • 性质2：若F1和F2都是A1 , A2 , …, An的函数，则 F=F1+F2将包括F1和F2中的公有最大项， G=F1·F2将包括F1和F2中的所有最大项。
  • 性质3：若F是F的反函数，则F必定由F所包含的最大项之外的全部最大项所组成。

1.2.3 逻辑函数的三种表示法的关系

用最小项表达式表示的逻辑函数，我们将原变量用1表示，反变量用0表示。这样我们把每个最小项都放进一个集合A里。那么，逻辑函数可以说是这个集合的特征函数。

同样的，用最大项表达式表示的逻辑函数，我们将原变量用0表示，反变量用1表示。这样我们把每个最大项都放进一个集合B里。那么，逻辑函数可以说是这个集合的特征函数。

从上一节的学习，我们知道逻辑函数有三种表示法：

  1. 逻辑表达式

  2. 真值表

  3. 卡诺图

首先，逻辑表达式形式都可以化成标准形式。

接着我们来看真值表与逻辑表达式的关系（最大/小项表达式也是逻辑表达式）：

还记得我们说最小项表达式可以看成是集合A的特征函数。而只要是在这个集合里的逻辑变量值的组合，其在真是表中的值都是1，不在这个集合里的逻辑变量值的组合都是0。

最大项表达式与最小项表达式恰恰相反：

最大项表达式可以看成是集合B的特征函数。而只要是在这个集合里的逻辑变量值的组合，其在真是表中的值都是0，不在这个集合里的逻辑变量值的组合都是1。

最后我们来看一下卡诺图与真值表的关系：

卡诺图其实是真值表的变形，真值表按照二进制顺序来排放逻辑变量值得组合：

1
2
3
4
5
6
7
8
——————————————
A  B	|	F
——————————————
0  0	|	0
0  1	|	1
1  0	|	1
1  1	|	0
——————————————

它是一维的 线性的。

而卡诺图则二维的：

将逻辑变量值得组合放在二维表格得行或列，每个行或列 填上不同的组合，这样每个格子就可以表示由这些变量所组成的所有最小项。

image-20220824175139560

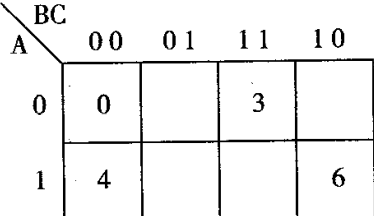
将项的组合换成数字的组合，我们得到卡诺图的简化形式

image-20220824175241939

需要注意的是，如上图所示：边框外的二进制数的排列数序并不是随意的，而是必须按照格雷码的顺序排列。

下面给出一个逻辑函数的卡诺图表示的例子：

image-20220824175443316

补充：格雷码

https://baike.baidu.com/item/%E6%A0%BC%E9%9B%B7%E7%A0%81/6510858

在一组数的编码中，若任意两个相邻的代码只有一位二进制数不同，则称这种编码为格雷码（Gray Code），另外由于最大数与最小数之间也仅一位数不同，即“首尾相连”，因此又称循环码或反射码。

递归生成码表

这种方法基于格雷码是反射码的事实，利用递归的如下规则来构造：

  1. 1位格雷码有两个码字
  2. (n+1)位格雷码中的前2n个码字等于n位格雷码的码字，按顺序书写，加前缀0
  3. (n+1)位格雷码中的后2n个码字等于n位格雷码的码字，按逆序书写，加前缀1 [4]
  4. n+1位格雷码的集合 = n位格雷码集合(顺序)加前缀0 + n位格雷码集合(逆序)加前缀1
2位格雷码 3位格雷码 4位格雷码 4位自然二进制码
00 000 0000 0000
01 001 0001 0001
11 011 0011 0010
10 010 0010 0011
110 0110 0100
111 0111 0101
101 0101 0110
100 0100 0111
1100 1000
1101 1001
1111 1010
1110 1011
1010 1100
1011 1101
1001 1110
1000 1111

第二次课结束

1.3 主要定理 & 常用公式

1.3.1个主要定理

德摩根律：

image-20220828210855685

  • 当变量个数较少的时候，可以使用真值表法证明。
  • 当变量较多的时候，使用数学归纳法证明。

香农定理： 任何函数的反函数，可通过对该函数的所有变量取反，并将1换成0，0换成1，· 换成 + ，+换成 · 运算得到。

image-20220828211532973

注意：我们使用香农定理是不能改变运算的顺序，而+ 和 ·的优先级不一样，因此如有必要需要加括号。

对偶定理:

对偶函数的定义：

将逻辑函数中的 · +互换 ，01互换，但变量不变，则函数变为原来的对偶函数

设原函数表示为 f (x1, x2, … , xn, 0, 1, +, · )

则其对偶函数为 f ‘ (x1, x2, … , xn, 0, 1, +, · ) = f (x1, x2, … , xn, 1, 0, ·, 1)

对偶定理表述为：对于任何函数的对偶函数，可以通过原函数的所有变量取反，并再对整个函数求反函数得到。

image-20220828212559479

两个推论：

  1. 原函数与其对偶函数互为对偶函数。
  2. 两个相等的函数（f = g）的对偶函数必定相等（f ‘ = g ‘）

自对偶函数：一个函数的对偶函数等于它自己。

展开定理：

image-20220828213000128

两个推理：

image-20220828213053195

展开定理可以用于将逻辑函数展开成 与或式 or 或与式。详见 P16

1.3.2 5个常用公式

  1. AB + A┐B = A

    在一个积之和表达式中，若有一个变量，他在一个乘积项中为原变量，在另一个乘积项中为反变量，且这两个乘积项的其余因子相同，则此变量是多余的。

  2. A + AB = A

    在一个积之和表达式中，若有一个乘积项是另一个乘积项的因子，则包含这个乘积项的乘积项是多余的。

    还可以写成ABC + ABCDE = ABC

  3. A + ┐AB = A + B

    在一个积之和表达式中，若有一个乘积项的“非”是另一个乘积项的因子，则在该乘积项中，这个因子是多余的。

    ┐C + CE = ┐C + E

  4. AB + ┐AC + BC = AB + ┐AC

    包含律

    在一个积之和表达式中，若有两个乘积项，其中一个包含原变量x另一个包含反变量┐x 且这两个乘积项的其余因子都是另一个乘积项的因子，则另一个乘积项是多余的。

    AB + ┐AC + BCDE = AB + ┐AC

  5. ┐(A┐B + ┐AB) = ┐A┐B + AB

    两个变量的异或的反 是 两个变量的同或

上面5个公式的对偶形式也是成立的

1.3.3 异或的性质

A ⊕A = 0

A⊕┐A = 1

A⊕0 = A

A⊕1 = ┐ A 重要

A⊕┐ B = A ⊙ B = A⊕B⊕1

A⊕B = B⊕A 交换律

A⊕(B⊕C) = （A⊕B) ⊕C 结合律

A(B⊕C) = AB⊕AC 分配律

第三次课到此结束

1.3.4 应用

一、转化称其他形式（详见P20）

  1. “与或” 表达式转 “或与”表达式

    法一：分配律

    法二：展开定理

  2. “与或” 表达式 转 “与非 - 与非” 表达式

    “与非 - 与非” 表达式 ：若干个“与非”项进行“与非”得到的逻辑表达式

    或与表达式是中间由 + 即或连接的，我们只要利用德摩根律将这个或变为与即可

    因此我们的步骤是：两次取反，内层非用德摩根律断开

  3. “与或” 表达式 转 “或非 - 或非” 表达式

    “或非 - 或非” 表达式: 若干个“或非”项进行“或非”得到的逻辑表达式

    首先将 “与或” 转换为 “或与”，再两次取反，内层非用德摩根律断开

二、最大项表达式和最小项表达式的关系

┐mi = Mi 或 mi = ┐Mi

mi’ = Mj，且i + j = 2 ** n - 1

image-20220829230044488

原函数

​ — 变换 —>

最小项表达式

​ — 一次取反 —>

符号错开，但保持最小项表达式，反函数的最小项表达式

或

或符号不错开，变成最大项表达式形式，得到反函数的最大项表达式形式

​ — 二次取反 —>

原函数的最大项表达式（和原函数最小项表达式符号错开）

将最大项表达式或最小项表达式变成对偶函数：

首先将最大项变成最小项，或最小项变成最大项

其次将序号变成互补的序号

1.4 逻辑函数的化简

逻辑函数最简式的定义：

  1. 该式中乘积项最少
  2. 该式中的乘积项不能再用变量更少的乘积项代替

化简方法:

  1. 代数方法
  2. 卡诺图法
  3. 列表化简法

1.4.1 卡诺图法

第四次课到此结束

基本原理：ABC + ┐ABC = (A + ┐A)BC = BC

反映在卡诺图上，就是相邻的两个格可以构成一个圈。

n变量的卡诺图，任何2^m^ 个标1的相邻单元可以形成一个圈，改圈所代表的乘积项由n-m个变量组成，可以消去m个变量。

名词解释：

蕴含项：最小项，以及2^m^ 个相邻单元所形成的圈组成的项。

素项：不是其他蕴含项子集的蕴含项。

实质素项：包含某一最小项，该最小项只被该素项包含。

化简方法：

  1. 作出卡诺图，找出全部素项

  2. 找出全部实质素项

  3. 若有未被覆盖的最小项，找出一个可以包含该最小项的蕴含项，将其添加到实质素项集合中。

    得到的集合，写成代数形式，即是化简结果。

第二章 组合电路的分析

2.1 各种门电路

或门

image-20220920125054365

与门image-20220920125108982

非门image-20220920125121515

与非门

image-20220920125145303

或非门

image-20220920125247085

与或非门

image-20220920125206325

异或门

image-20220920125225775

三态门

image-20220920125344236

三态门真值表：

E A F
0 0 0
0 1 1
1 任意 高阻抗

第五次课结束

2.2 门电路的主要参数以及组合电路的分析方法

门电路的主要参数：

  • 标称逻辑电平：表示逻辑值01的理想电平

  • 扇入系数：门电路允许的输入端数目

    若使用的输入端数目比扇入系数小，则多余的输入端再不改变电路逻辑功能的情况下接高电平或低电平

  • 扇出系数：一个门电路输出端所连接的下一级输入端的个数

  • 平均时延

组合电路的分析方法：

  1. 给定组合线路
  2. 列写逻辑表达式
  3. 列真值表
  4. 指出线路的逻辑功能
  5. 对线路进行评价和改进

2.3 全加器

符号表示：

  • A 被加数
  • B 加数
  • C~i-1~ 低位向高位的进位
  • S 和

全加器的逻辑符号：

image-20220920130348535

image-20220920130415100

S = A⊕B⊕C~i-1~

​ = ∑(1, 2, 4, 7)

C = AB+(A⊕B)C~i-1~
= AB+(A+B)C~i-1~

​ = ∑(3, 5, 6, 7)

2.4 译码器

几种常见的十进制数在二进制下的编码：

  • 8421码：顾名思义，就是十进制数转直接转换成二进制数（范围是0000-1001）

  • 格雷码：相邻的格雷码只有一个位不同

    8421转格雷码：G~i~=B⊕B~i+1~ (i <= n-1); G~i~ = B~i~ (i = n)

  • 余三码：8421码+3得到余三码（范围是0011-1100）

十进制数 8421 格雷码 余三码
0 0000 0000 0011
1 0001 0001 0100
2 0010 0011 0101
3 0011 0010 0110
4 0100 0110 0111
5 0101 0111 1000
6 0110 0101 1001
7 0111 0100 1010
8 1000 1100 1011
9 1001 1101 1100

第五次课结束

不同的译码器：

三位译八位译码器（多一译码）：从三位二进制数中，翻译出他们的最小项表达式。

高电平译重：翻译出来的那个最小项的电平是高电平

低电平译重：翻译出来的最小项的电平是低电平

如果使用与非门实现译码器，使用低电平译重可以节省非门

2.5.格雷码转8421码：

利用异或的性质，一个逻辑表达式异或同一个逻辑表达式两次，等于原逻辑表达式

已知从8421码到格雷码的转换有：

G0 = B0 ⊕ B1

G1 = B1 ⊕ B2

G2 = B2 ⊕ B3

G3 = B3

则根据异或的性质

  1. B3 = G3 已知

  2. G2 = B2 ⊕ B3 已知

  3. G2 = B2 ⊕ G3 （2）

  4. G3 ⊕ G2 = B2 ⊕ G3 ⊕ G3 两边同时异或G3
  5. B2 = G2 ⊕ G3 异或的性质，消去两个G3

于是我们有：

从格雷码到8421码：

B3 = G3

B2 = G2 ⊕ G3

B1 = G1 ⊕ G2 ⊕ G3

B0 = G0 ⊕ G1 ⊕ G2 ⊕ G3

2.6 奇偶校验器

分为奇校验和偶校验：

我们有一个n位二进制数和一个校验位p

奇校验：n位二进制数和p中，1的个数是奇数

偶校验：n位二进制数和p中，1的个数是偶数

奇偶校验的原理：

n个二进制数异或，如果他们中1的数目是奇数，则结果为1

这个原理可以使用数学归纳法证明

一个逻辑变量异或1等于它的非

一个逻辑变量异或0等于它本身

下面以奇校验为例：

生成校验位:

p = B8 ⊕ B4 ⊕ B2 ⊕ B1 ⊕ 1

校验

is_valid = B8 ⊕ B4 ⊕ B2 ⊕ B1 ⊕ P

偶校验

p = B8 ⊕B4 ⊕B2 ⊕B1

校验

is_valid = B8 ⊕B4 ⊕B2 ⊕B1⊕p⊕1

第三章 组合线路的设计

设计流程：

  1. 确定逻辑功能
  2. 列真值表（也就得到了最小项表达式）
  3. 根据卡诺图化简逻辑表达式
  4. 按照设计要求变换逻辑表达式
  5. 考虑工程问题

3.1 逻辑函数的变换

与或变与非：

  1. 两次取反，中间DM断开
  2. 对F的反函数，三次取反（可以理解为四次取反，怎样好用用那个）

与或非：

  1. 两次取反，不断开
  2. 对反函数一次取反

或非

  1. 首先将 “与或” 转换为 “或与”，再两次取反，内层非用德摩根律断开

  2. 首先将原函数转换成其对偶函数，再将对偶函数化成最小项表达式，两次取反转换成与非形式

    在进行一次对偶，变回原函数，得到或非形式

第六次课结束

3.2 利用任意项的线路设计

任意项定义：是的约束方程推的逻辑值为0的最小项，也称无关项。

任意项再当前约束条件下的逻辑值必定为0，因此我们将任意项和原函数进行或运算，不影响原函数的取值。

任意项在卡诺图或真值表中，用φ表示，将它在卡诺图中画出来可以方便形成更大的圈，从而简化得到的逻辑表达式。但我们使用真值表化简带有任意项的逻辑函数时，不必考虑任意项是否被圈全部包含，只需要考虑逻辑函数的最小项。

3.3 多输出函数的线路设计（需要考虑共享项）

当我们有多个逻辑函数，共享输入时，我们需要从全局出发考虑，看是否有可以共享的项目，从而减少要使用的逻辑器件。

考虑共享项的最小覆盖修改原则：

  1. 若F~i~的一个素项B~k~也是F~j~的一个素项，则B~k~不作修改，除非修改后能减少总圈数。

  2. 若B~i~、B~j~分别是F~i~、F~j~的素项，且B~i~、B~j~都包含一个蕴涵项B~k~,在选取B~k~后，B~i~、B~j~中余下的最小项均分别包含在F~i~、F~j~其它素项中，则在F~i~、F~j~中改选B~k~

    示例：

    image-20221003100116410

  3. F~i~的一个素项B~i~，中的一些最小项分别被F~j~, F~j+1~, … , F~j+m~中的素项B~j~, B~j+1~ , … , B~j+m~覆盖，且B~j~, B~j+1~, … , B~j+m~ ⊆ B, 若在F~i~中选取B~j~,B~j+1~, …, B~j+m~ 后，B~i~中余下的最小项均包含在的其它素项中，则将B~i~改选为B~j~, B~j+1~, …, B~j+m~

    示例：

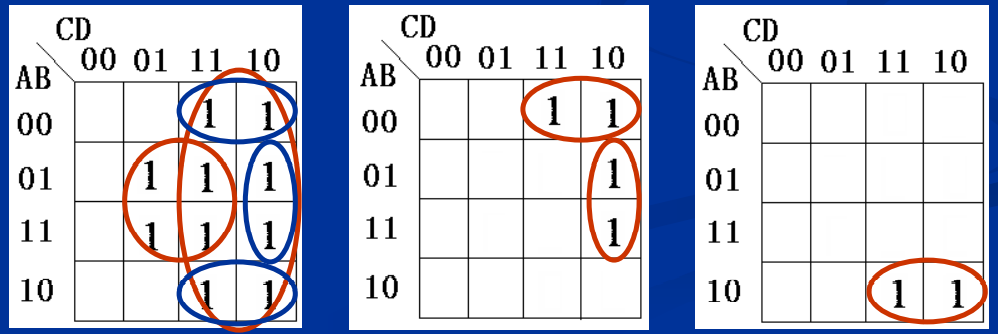
    image-20221003100828764

第七次课到此结束

3.4 应用MSI功能块的组合线路设计

SSI：小规模集成电路

MSI：中规模集成电路

  • 利用数据多路选择器进行设计

    首先要知道数据多路选择器的原理

    f = a~0~┐x~0~┐x~1~ + a~1~┐x~0~x~1~ + a~2~x~0~┐x~1~ + a~3~x~0~x~1~

    设计步骤：

    1. 首先，对于给定n变量的逻辑函数，我们选择N = 2^n-1^ 路数据选择器

    2. 选定n-1个变量作为地址输入，作为数据选择器的控制端，根据选择的地址输入，确定数据选择器输入端的各表达式输入

      对于如何确定数据选择器输入端的各表达式，我们可以使用代数方法得到，也可以使用卡诺图方法得到。

  • 利用译码器进行线路设计

    将对应逻辑表达式转换为最小项表达式，直接将译码出来的最小项用或门连接（高电平译中）或用与非门连接（低电平译中），输出即可。

第八次课到此结束

第四章 时序电路的分析

4.1 触发器的外特性

4.1.1 基本触发器

基本触发器通过其电路的设计，可以具有存储二进制位的功能，其电路就是存储器，而不是有单独的存储器。

基本触发器有两个稳态，分别表示0和1。当基本触发器（R~D~ ，S~D~）输入 1，1时，基本触发器里存储的位被保持输出，当输入0，1时，基本触发器被置零，当输入1，0时，基本触发器被置一，当输入0，0时不能确定输出的是当前存储的状态，还是其他状态。因此不能输入0。

基本触发器的R~D~ 和S~D~ 端都是低电平有效，R端是Reset重置，置零端，S端是Set，置一端。

基本触发器的特征表达式

┐R~D~┐ S~D~ = 0 (R~D~ 和S~D~ 不能同时为0)

Q^n+1^ = ┐S~D~ + R~D~ Q

4.1.2 RS触发器

电位触发，高电位时触发

五个输入端，R~D~ , S~D~ ，R, S, CP

CP只有在为1时才有效，CP为0时保持。

特征方程：

Q^n+1^ = S + ┐RQ

4.1.3 D 触发器

边缘触发器，正跳变触发

关于电位触发和边缘触发：

边缘触发：输出不能迟于触发信号到达，但触发信号已到达，输入信号就可以撤下来

电位触发：输入信号可以迟于触发电位到达，但在触发电位变回非触发电位前，输入信号不能改变

Q^n+1^ = D

4.1.4 JK 触发器

边缘触发器，负跳变触发

Q^n+1^ = J ┐Q^n^ + ┐K Q^n^

当J，K同为0时，输出Q

当J，K同为1时，输出┐Q

当J，K相异时，输出 J

4.1.5 T触发器

边缘触发器，负跳变触发

Q^n+1^ = T┐Q^n^ + ┐TQ^n^

当T为0时，输出Q

当T为1时，输出┐Q

第九次课到此结束

4.2 时序电路的分析方法

  1. 列些输出函数和控制函数表达式

    输出函数：线路的外输出函数（z）

    控制函数：向存储元件的输入

  2. 建立次态表达式及状态转移表

  3. 建立状态表及状态图

  4. 画波形图（optional）

  5. 说明时序线路的功能

异步电路分析：

  1. 写出输出函数和控制函数和每个触发器的CP端
  2. 建立次态表达式，次态表达式要将CP写进去，注意，不同触发器CP为一的条件不同
  3. 建立状态转移，如果输入信号是脉冲信号，那么输入信号为一代表打一个脉冲，而非输入信号恒唯一。
  4. 建立状态表和状态图
  5. 画波形图
  6. 说明时序电路功能

第十&十一次课到此结束

4.3 同步时序电路的设计

同步时序电路设计的一般步骤：

  1. 根据问题的描述，建立原始的状态表
  2. 使用隐含表法（下三角矩阵）化简原始状态表
  3. 对最简状态表进行编码，建立编码状态表
  4. 画出真值表（包括外部输入，现态，次态，控制函数，输出）
  5. 根据真值表写出触发器的控制函数
  6. 设计组合线路，考虑工程问题

4.3.1 关于状态的化简

两个状态可以合并的条件：

  1. 在所有不同的输入下，输出均相同且满足以下条件
    1. 两个次态完全相同
    2. 两个次态为其现态的交错
    3. 两个次态的某一后续状态对可以合并
    4. 两个次态为状态对封闭链中的一个状态对。

本课程结束